《分数与整数相乘》教学设计

教学内容：教材第38～39页例1，练一练和练习八第1～5题

【教学目标】
1．让学生通过自主探索，了解分数与整数相乘的意义，知道“求几个几分之几相加的和”可以用乘法计算，初步理解和掌握分数与整数相乘的计算方法。
2．让学生进一步增强运用已有知识和经验探索并解决问题的意识，体验探索学习的乐趣，培养学生迁移、类推、独立探究的能力和敢于尝试的精神。
3．渗透事物是相互联系、相互转化的辩证唯物主义观点。
教学重、难点
1．重点：掌握分数与整数相乘的计算方法，会正确计算。
2．难点：理解分数与整数相乘的意义。

【阅读+理念的体现】借助情境图的阅读与理解，培养学生阅读文本材料，捕捉数学信息的能力，初步形成用完整的较为科学的语言描述图意的能力，准确把握关键信息并初步形成能结合具体情境描述具体问题。

2.学生经历数学学习的过程，相互交流、讨论和自我反思，感受数学与生活密切联系与价值。

3.利用阅读帮助学生了解数学知识的起源与背景，提升学生阅读和学习的兴趣。

一、复习导入

1.看到这个课题，你能说说我们曾经学过哪些乘法吗？

整数乘法，小数乘法

今天呢，我们就一起来研究未曾学过的分数乘法

2.复习：6个3相加的和是多少？

6×3=18

整数乘法的意义是什么？

是加法的简便运算；不错，是求几个相同加数的和的简便运算

3.我们继续来复习一下有关分数加法的知识

第一题的结果是？

谁来说说分数加法是如何计算的？分母不变，分子相加

第二题的结果是？，

到底是还是？

求出的结果需要怎么样？化简（约分）

4. 仔细观察，这题（第二题）的每个加数有什么特点？全都一样

你想想第二个算式有没有更简便的算法呢？有（×3）

这就是我们今天要学的内容——分数与整数相乘（板书）

二、新课探究

5. 出示例1，谁来读一下题目？xx读题

我们用这根直条表示1m长的绸带，那么m在图中表示多长呢？你怎么理解？

把1m平均分成10份，给其中的3份涂上颜色，就表示m长的绸带。

6. 做3朵这样的绸花所用的米数你能在图中涂色表示出来吗？能

怎么涂？再涂6格；一共涂9格；涂到最后差一格......

7. 你会列式表示吗？你能说说你的思考过程吗？

×3=

a：×3就是表示3个相加，3个相加可以写成++=（联系同分母分数连加来思考）

b：就是3个，×3就是9个，也就是，（联系分数的意义思考）

8. 指出：刚才同学们的想法虽然不同，但都是把3个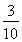合起来，都可以用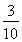++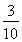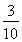=来计算。（沟通不同思路之间的内在联系）

9.仔细观察，++=，3个3相加，还可以怎样表示？3×3

所以++==

10.回顾：根据大家的讨论，你能归纳一下×3怎么计算吗？

归纳：计算×3时，分母不变，用3×3的积作积的分子（分子×整数的积作积的分子）

你会做这类题目了吗？我们继续来尝试一下

出示例1（2），小华，做五朵这样的绸花，一共需要用绸带几分之几米？

学生独自完成，教师巡视

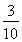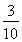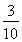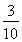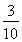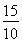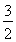1. ++++====（5个3相加可以写成5×3的形式）

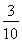2. ×5=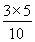==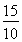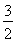（分子和整数相乘的结果有可能较大，我们可以提前约分）

11. 你是怎样列式的，为什么可以这样列式？

明确：可以先约分再计算

12. 引导：比较刚才两道乘法算式的过程，您能总结归纳一下，分数和整数相乘，该怎样计算呢？

13. 小结：分数与整数相乘，要用分数的分子与整数相乘的积作分子，分母不变。计算时，能约分的，要先约分再计算。

三、巩固提高

14. 练习五1

让学生看图说说题意，再独立完成填空，并组织反馈。

追问：题中的×2可以表示什么？

指出：求几个相同分数的和，可以用乘法计算。

15. 做“练一练”第一题

学生先按要求在正方形中涂色，再列式计算。

交流学生的算法和结果，并与图中涂色部分进行对比，确定计算结果。

提问：求4个是多少，为什么可以用乘法计算？

16. 做“练一练”第二题

学生计算时，注意提醒学生：能约分的要先约分再计算。

17. 练习五3，4

让学生独立解答，再说说解题时的思考过程

指出：求几个分数相加的和，可以用乘法计算。

四、回顾总结

提问：今天这节课我们学习了什么内容？是怎样得出分数与整数相乘的计算方法的？你还有哪些收获和体会？

五、课堂作业

练习五2,5

【教学反思】分数乘整数的知识基础在于同分母分数加法的计算方法及分数的意义及整数乘法的意义等知识。在课前,我对这些内容进行了一定的复习,再进入分数乘整数的教学。

分数乘整数的算法很简单,在相乘时,分母不变,只把整数和分数的分子相乘的积作分子。在教学这个内容时,我关注到新教材在算理方面的重视,注意到图形和算式之间的联系,在计算前充分让学生感知画、涂图形的过程。因此,在后面计算方法的得出就水到渠成,比较容易了。再者,对“分数乘整数表示的意义”也有机的渗透,为后面的知识打好铺垫。

一堂课上下来,由于学生对内容比较容易接受,课堂上有了空余时间。学生对算理的理解比较清晰,但还存在的问题就是约分的环节,有些学生喜欢算出结果以后再约分,对计算过程约分还不愿意采用。

这一环节还应讲深讲透。学生可能对于这种在计算过程当中的约分,还是一知半解,对这样约分的道理理解得不够清楚。学习分数乘整数,学生在计算时肯定会遇到先约分后乘还是先乘后约分的问题。如果仅仅是为得到一个正确的结果,那么无论前者,还是后者,都无关紧要,只要不出差错,最后都能得到正确结果。显然,我们还需要学生养成良好的计算习惯,较高的计算速度和计算正确率!那么我们就必须让学生明白到底哪种思路更合理,更有助于自己的后续学习。作为分数乘法的第一节课—分数乘整数,形成先约分后计算的良好计算习惯,对于提高学生计算的正确率和计算速度,有着很重要的作用。在教学分数乘法过程中约分时,我让学生用两种方法进行了比赛,如果哪位学生是用整数直接乘以分子的,速度当然会很慢,当做得最快的同学展示自己的做法时,其他同学恍然大悟,深刻体会到计算过程中先约分,可以化繁为简。这样,学生在做分数乘法时,不仅仅满足于“分子和整数相乘的积作分子,分母不变”,而是记住“能约分的要先约分”这一要点。